Fortran has good facilities for processing numbers. Arithmetic expressions and assignment statements can include integer, real, double precision, or complex items. Data type conversions are provided automatically when necessary; type conversions can also be performed explicitly using intrinsic functions. Other intrinsic functions are available for trigonometry, logarithms, and other useful operations.
For example, the well-known cosine formula for the third side of a triangle, given the other two sides and the angle between them is:
![]()
Translated into a Fortran expression it looks like this:
SQRT(B**2 + C**2 - 2.0 * B * C * COS(ANGLEA))
which makes use of the intrinsic functions SQRT and COS.
Although SQRT(X) produces the same result as X**0.5, the
square-root function is simpler, faster, and probably more accurate
than raising to the power of one half, which would actually be
carried out using both the EXP and LOG functions.
Assignment statements evaluate an expression and assign its value to a variable (or array element). Unlike almost all other Fortran statements, they do not start with a keyword. For example:
A = SQRT(B**2 + C**2 - 2.0 * B * C * COS(ANGLEA))
TOTAL(N/2+1) = 0.0
FLUX = FLUX + 1.0
An expression in its simplest form is just a single operand, such as
a constant or variable. More complicated expressions combine
various operands with operators, which specify the computations
to be performed. For example:
RATE * HOURS + BONUS
The rules of Fortran have been designed to resemble those of
mathematics as far as possible, especially in determining the order
in which the expression is evaluated. In this example the
multiplication would always be carried out before the addition, not
because if comes first, but because it has a higher precedence.
When in doubt, or to over-ride the precedence rules, parentheses
can be used:
(ROOM + DINNER) * 1.15
Sub-expressions enclosed in parentheses are always evaluated first; they can be nested to any reasonable depth. If in doubt, there is no harm in adding parentheses to determine the order of evaluation or to make a complicated expression easier to understand.
Arithmetic expressions can contain any of the five arithmetical
operators + - * / ** .
The double asterisk represents exponentiation, i.e. raising a
number to a power. Thus the mathematical expression:
![]()
could be represented in Fortran as:
(1.0 + RATE/100.0)**YEARS
(note the explicit decimal points in the constants to make them real
values).
Arithmetic expressions can involve operands of different data types: the data type of the result is determined by some simple rules explained below.
Arithmetic expressions can contain arithmetic operands, arithmetic operators, and parentheses. There must always be at least one operand. The operands can belong to any of the four arithmetic data types (integer, real, double precision, or complex); the result also has an arithmetic data type. Operands can be any of the following:
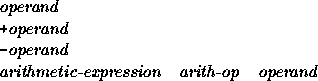

The effect of these rules is that an expression consists of a string of operands separated by operators and, optionally, a plus or minus at the start. A leading plus sign has no effect; a leading minus sign negates the value of the expression.
All literal arithmetical constants used in expressions must be
unsigned: this is to prevent the use of two consecutive operators
which is confusing and possibly ambiguous:
4 / -3.0**-1 (illegal).
The way around this is to use parentheses, for example:
4 / (-3.0)**(-1)
which makes the order of evaluation explicit.
The order of evaluation of an expression is:
Within each of these groups evaluation proceeds from left to right, except that exponentiations are evaluated from right to left. Thus: A / B / C is equivalent to (A / B) / C whereas X ** Y ** Z is equivalent to X ** (Y ** Z).
An expression does not have to be evaluated fully if its value can
be determined otherwise: for example the result of:
X * FUNC(G)
can be determined without calling the function FUNC if X happens
to be zero. This will not cause problems if you only use functions
that have no side effects.
If an operator has two operands of the same data type then the
result has the same type. If the operands have different data types
then an implicit type conversion is applied to one of them to bring
it to the type of the other. These conversions always go in the
direction which minimises loss of information:
Since there is no way of converting a complex number to double precision type, or vice-versa, without losing significant information, both these conversions are prohibited: an operator cannot have one complex operand and one of double precision type. All other combinations are permitted. These implicit type conversions have the same result as if the appropriate intrinsic function (REAL, DBLE, or CMPLX) had been used. These are described in detail below. Note that the data type of any operation just depends on the two operands involved; the rest of the expression has no influence on it whatever.
Exponentiation is an exception to the type conversion rule: when
the exponent is an integer it does not have to be converted to the
type of the other operand and the result is evaluated as if by
repeated multiplication. But if the exponent has any other data
type the calculation is performed by implicit use of the LOG and
EXP functions, thus:
The first result will, of course, be computed more rapidly and
accurately than the second. If the exponent has a negative value
the result is simply the reciprocal of the corresponding positive
power, thus:
Note that conversion from real to double precision cannot produce any information not present originally. Thus with a real variable R and a double precision variable D:
R = 1.0 / 3.0
D = R
D may end up with a value such as 0.3333333432674408... which
is no closer to the value of one third than R was originally.
Integer division always produces a result which is another integer
value: any fractional part is truncated, i.e. rounded towards zero.
This makes it especially important to provide a decimal point at the
end of a real constant even if the fractional part is zero. For
example:
The combination of the two preceding rules may have unexpected
effects, for example:
whereas (-2)**3.0 is an invalid expression as the computer would
try to evaluate the logarithm of -2.0, which does not exist.
Similarly, the expression:
whereas
Certain arithmetical operations are prohibited because their results are not mathematically defined. For example dividing by zero, raising a negative value to a real power, and raising zero to a negative power. The Fortran Standard does not specify exactly what is to happen if one of these errors occurs: most systems issue an error message and abort the program.
Errors can also occur because numbers are stored on a computer with finite range and precision. The results of adding or multiplying two very large numbers may be outside the number range: this is called overflow. A similar effect on very large negative integers is called underflow. Most systems will issue a warning message for overflow or underflow, and may abort the program, but some processors cannot detect errors of this sort involving integer arithmetic.
Every operand (variable, array element, or function reference) used in an expression must have a defined value at the time the expression is evaluated. Note that variables and arrays are initially undefined unless a suitable DATA statement is used. Expressions must not include references to any external functions with side effects on other operands of the expression: see section 9.3 for more details.
Arithmetic constant expressions can be used in PARAMETER statements and to specify implied-DO parameters in DATA statements. All the operands in a constant expression must be literal constants or previously defined named constants. Variables, array elements, and function references are all prohibited. Exponentiation is only allowed if the number is raised to an integer power.
The same rules apply to integer constant expressions but in addition the operands must all be integer constants: such expressions can be used to specify array bounds in type, COMMON, and DIMENSION statements, and to specify string lengths in CHARACTER statements.
When Fortran programs communicate directly with digital hardware it may be necessary to carry out bit-wise logical operations on bit-patterns. Standard Fortran does not provide any direct way of doing this, since logical variables essentially only store one bit of information and integer variables can only be used for arithmetic. Many systems provide, as an extension, intrinsic functions to perform bit-wise operations on integers. The function names vary: typically they are IAND, IOR, ISHIFT. A few systems provide allow the normal logical operators such as .AND. and .OR. to be used with integer arguments: this is a much more radical extension and much less satisfactory, not only because it reduces portability, but also reduces the ability of the compiler to detect errors in normal arithmetic expressions.
Many systems also provide format descriptors to transfer integers using octal and hexadecimal number bases: these are also non-standard.
Expressions with mixed data types should be examined carefully to ensure that the type-conversion rules have the desired effect. It does no harm to use the type conversion functions explicitly and it may make the working clearer.
Particular care is needed with the data types of literal constants. It is bad practice to use an integer constant where you really need a real constant. Although this will work in most expressions it is a serious mistake to use the wrong form of constant in the argument list of a procedure.
Long and complicated expressions which spread over several lines can be rather trying to read offer more scope for programming errors. Sometimes it is better to split the computation into several shorter equations at the expense of one or two temporary variables.
It is often tempting to try to write programs that are as efficient as possible. With modern compilers there is little point in trying to rearrange expressions to optimise speed. One of the few exceptions is that if an intrinsic function is provided it is always best to use it; thus SQRT(X) is likely to be faster and more accurate than X**0.5.
You may find that your system actually sets the whole of memory to zero initially, except for items defined with DATA statements, but it is very bad programming practice to rely on this.
Intrinsic functions are supplied automatically by the system and can be used in expressions in any program unit. A description of their special properties appears in section 9.1.
Many of the arithmetic intrinsic functions have generic names: that is they can be used with several different types of arguments. The SQRT function, for example, can be used with a real, double precision, or complex argument. The Fortran system automatically selects the correct specific function for the job: SQRT, DSQRT, or CSQRT. These specific names can be ignored in almost all circumstances, and are listed only in the appendix. In most cases the data type of the function is the same as that of its argument but there are a few obvious exceptions such as the type conversion functions.
In the descriptions below, the number and data type of the arguments of each intrinsic function are indicated by a letter: I = integer, R = real, D = double precision, X = complex.
An asterisk on the left indicates that the result has the same data type as the arguments. Note that if multiple arguments are permitted they must all have the same data type. Thus I = NINT(RD) indicates that the NINT function can take a single real or double precision argument but its result is always integer, whereas * = ANINT(RD) indicates that the result has the same type (real or double precision) as the argument.
The functions in this group can all be used on real or double precision arguments, and SIN and COS can also be used on complex numbers. In every case the result has the same data type as the argument.

Note that the arguments of SIN, COS, and TAN must be angles
measured in radians (not degrees). They can be used on angles of
any size, positive or negative, but if the magnitude is very large the
accuracy of the result will be reduced. Similarly all the inverse
trigonometric functions deliver a result in radians; the argument of
ASIN and ACOS must be in the range -1 to +1.
The ATAN2 function can be useful in resolving a result into
the correct quadrant of the circle, thus:
ATAN(0.5) = 0.4636476
ATAN2(2.0,4.0) = 0.4636476
ATAN2(-2.0,-4.0) = -2.677945 ( = 0.4636476 - ![]() ).
).

Note that LOG10, which may be useful to compute decibel ratios etc., is the only one of this group which cannot be used on a complex argument.
These functions can be used to convert from any of the four arithmetic data types to any of the others. They are used automatically whenever mixed data types are encountered in arithmetic expressions and assignments.

The integer conversion of INT rounds towards zero; if you need to round to the nearest integer use the NINT function (described below). The CMPLX function produces a value with a zero imaginary component unless it is used with two arguments (or one which is already complex). It is important to realise that many conversions lose information: in particular a double precision value is likely to lose significant digits if converted to any other data type.
The MIN and MAX functions are unique in being able to take any number of arguments from two upwards; the result has the same data type as the arguments.
![]()
These two functions can, of course, be combined to limit a value
to a certain range. For example, to limit a value TEMPER to the
range 32 to 212 you can use an expression such as:
MAX(32.0, MIN(TEMPER, 212.0))
Note that the minimum of the range is an argument of the MAX
function and vice-versa.
To find the largest (or smallest) element of a large array it is necessary use a loop.
*Find largest value in array T of N elements:
TOP = T(1)
DO 25,I = 2,N
TOP = MAX(T(I), TOP)
25 CONTINUE
*TOP now contains the largest element of T.

The NINT and ANINT functions round upwards if the fractional
part of the argument is 0.5 or more, whereas INT and AINT always
round towards zero. Thus:
INT(+3.5) = 3 NINT(+3.5) = 4
INT(-3.5) = -3 NINT(-3.5) = -4
The fractional part of a floating point number, X, can easily be
found either by:
X - AINT(X)
or
MOD(X, 1.0)
In either case, if X is negative the result will also be negative. The
ABS function can always be used to alter the sign if required.
The MOD function has other uses. For example it can find the day
of the week from an absolute day count such as Modified Julian
Date (MJD):
MOD(MJD,7)
has a value between 0 and 6 for days from Wednesday to Tuesday.
Similarly if you use the ATAN2 function but want the result to lie
in the range 0 to 2ã (rather than -ã to +ã) then, assuming the
value of TWOPI is suitably defined, the required expression is:
MOD(ATAN2(X,Y) + TWOPI, TWOPI)
An arithmetic assignment statement has the form:
arithmetic-var = arithmetic-expression
where arithmetic-var can be an arithmetic variable or array
element. For example, the following assignment statement is valid
provided that N, K, and ANGLE are all defined values:
IMAGE(N/2+1,3*K-1) = SIN(ANGLE)**2 + 1.0
If the object on the left has a different data type from that of the
expression on the right then a data type conversion is applied
automatically. The type conversion function (INT, REAL, DBLE,
or CMPLX) is selected to match the object on the left. Note that
many type conversions lose information. If the object on the left
is an array element, its subscripts can be arbitrary integer
expressions, but all the operands in these expressions must be
defined before the statement is executed and each must be in the
range declared for the corresponding subscript of the array.
Remember with an integer item on the left and an expression of one of the floating-point types, the INT function is invoked: if the NINT function is really needed then it must be used explicitly to convert the value of the expression.